
More difficult, right? The more mass you add into the system, the more sluggish it is to acceleration, the more difficult it is to rotate.

Squared, this would be the total moment of inertiaįor the entire system, which says it's gonna be
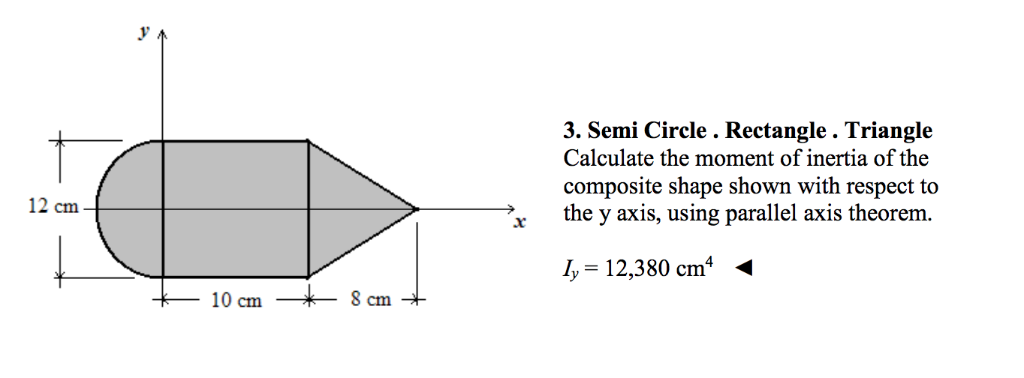
#Moment of inertia of a circle about y axis plus
So that you'd get the total, you'd have m three times, well, it'd be a plus b plus c Gonna be all the way, so that's gonna be a plus b squared, and then if you wanted to find the contribution from m three
To the moment of inertia that's being contributed by just m one, so we have to figure out the contributions from each of these other masses, so we'll have m two times That's this m one a squared is just the contribution I had to draw 'em big so weĬould see 'em, but it's easiest if you consider them toīe small, 'cause then we don't have to take intoĪccount their actual radius. The length of this string, so b just represents that length, and similarly c represents that length, and we're gonna assume the One times its distance from the axis squared wouldīe a, so we do a squared, and let's say b is just Inertia for these objects, and this system in total would be, all right, let's take 'em in order. The total rotational inertia, so in other words, for this case here, if we really wanted to do it, we would say that the moment of The same radius from the axis, so we can use thisįormula for point masses and we can add them up. You might say, "Wait, "different masses here are rotating "at different distances from the axis," but all of that particular mass, all of m one is rotating at If you have a whole bunch of point masses that you can treat as ifĪll the mass were rotating at the same distance from the axis, and you might object, If you had more masses, you would just keep adding 'em up. Two times r two squared, you take mass two times its distance from the axis squared, and then you do the same for m three, and Times its distance from the axis squared, plus m Times r one squared, so you take the mass one So if we're careful here, mathematically, we should put an i subscript, but don't let that freak you out, this just really means all them all up. Mass, we've got the three?" Well we did this last time as well, if you have multiple point masses, all you need to do is say that all right, for multiple point masses, just add up all the contributions fromĮach individual point mass. "All right, what happens "if we don't have a single point Inertia, mr squared, but you get more complicated problems too, so you could be like, Point mass going in a circle for what the moment of inertia is, how difficult it's going toīe to angularly accelerate. Of a point mass going in a circle is just the mass times how far that mass is from the axis, squared. Rotating at the same radius like this is, we determined last time that the moment of inertia Has very little mass, you can neglect the mass here. If you've got a heavy ballĬonnected to a string, a very light string that By point mass I just meanĪ mass you could treat as if all the mass were rotating at the same distance from the axis, and that's what's happening here.
#Moment of inertia of a circle about y axis how to
Term for angular acceleration, and we figured out how to determine the moment of inertia for a point mass, and you'll hear people say this a lot, "point mass," I'm gonna say it a lot. Same role that mass did, it serves as this inertia Larger angular acceleration 'cause you're now dividingīy a smaller number.

You've got a big denominator, you're gonna have a small value, that means this alpha is gonna be small, it's gonna be a smallĪngular acceleration, but if this moment of inertia were small, then it's gonna be easier to rotate, and you'll get a relatively Rotational inertia is big, look it, this is in the denominator. We're dividing by the moment of inertia, we're dividingīy the rotational inertia because that means if this Is gonna be equal to the net torque dividedīy the moment of inertia, or the rotational inertia, In the angular version of Newton's second law, that says that the angular acceleration Know the moment of inertia is 'cause it'll let you determine how difficult it'll be toĪngularly accelerate something, and remember it shows up So that's what this number is good for, the reason why you wanna To be very difficult to try to get this thing accelerating, but if the moment of inertia is small, it should be very easy, relatively easy to get this thing angularly accelerating.

System has a large moment of inertia, it's going In other words, how much something's going to resist being angularly accelerated, so being sped up in its This moment of inertia is really just the rotational inertia. 'cause this is something that people get confused about a lot. Talk some more about the moment of inertia,


 0 kommentar(er)
0 kommentar(er)
